Circle

A circle is a simple closed shape. It is the set of all points in a plane that are at a given distance from a given point, the centre; equivalently it is the curve traced out by a point that moves so that its distance from a given point is constant. The distance between any of the points and the centre is called the radius. This article is about circles in Euclidean geometry, and, in particular, the Euclidean plane, except where otherwise noted.

Circle
A circle (black), which is measured by its circumference (C), diameter (D) in cyan, and radius (R) in red; its centre (O) is in magenta.

A circle is a simple closed curve that divides the plane into two regions: an interior and an exterior. In everyday use, the term "circle" may be used interchangeably to refer to either the boundary of the figure, or to the whole figure including its interior; in strict technical usage, the circle is only the boundary and the whole figure is called a disc.

A circle may also be defined as a special kind of ellipse in which the two foci are coincident and the eccentricity is 0, or the two-dimensional shape enclosing the most area per unit perimeter squared, using calculus of variations.

Euclid's definition

A circle is a plane figure bounded by one line, and such that all right lines drawn from a certain point within it to the bounding line, are equal. The bounding line is called its circumference and the point, its centre.

History

The compass in this 13th-century manuscript is a symbol of God's act of Creation. Notice also the circular shape of the halo.

The word circle derives from the Greek κίρκος/κύκλος (kirkos/kuklos), itself a metathesis of the Homeric Greek κρίκος (krikos), meaning "hoop" or "ring".^[2] The origins of the words circus and circuit are closely related.

Circular piece of silk with Mongol images

Circles in an old Arabicastronomical drawing.

The circle has been known since before the beginning of recorded history. Natural circles would have been observed, such as the Moon, Sun, and a short plant stalk blowing in the wind on sand, which forms a circle shape in the sand. The circle is the basis for the wheel, which, with related inventions such as gears, makes much of modern machinery possible. In mathematics, the study of the circle has helped inspire the development of geometry, astronomy and calculus.

Analytic results

Length of circumference

The ratio of a circle's circumference to its diameter is π (pi), an irrational constant approximately equal to 3.141592654. Thus the length of the circumference C is related to the radius r and diameter d by:

${\displaystyle C=2\pi r=\pi d.\,}$

Area enclosed

Area enclosed by a circle = π × area of the shaded square

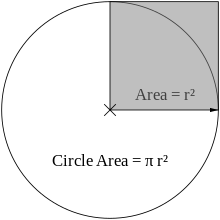
As proved by Archimedes, in his Measurement of a Circle, the area enclosed by a circle is equal to that of a triangle whose base has the length of the circle's circumference and whose height equals the circle's radius,^[7]which comes to π multiplied by the radius squared:

${\displaystyle \mathrm {Area} =\pi r^{2}.\,}$

Equivalently, denoting diameter by d,

${\displaystyle \mathrm {Area} ={\frac {\pi d^{2}}{4}}\approx 0{.}7854d^{2},}$

that is, approximately 79% of the circumscribing square (whose side is of length d).

The circle is the plane curve enclosing the maximum area for a given arc length. This relates the circle to a problem in the calculus of variations, namely the isoperimetric inequality.

Equations

Cartesian coordinates

Circle of radius r = 1, centre (a, b) = (1.2, −0.5)

Equation of a circle
In an x–y Cartesian coordinate system, the circle with centre coordinates (a, b) and radius r is the set of all points (x, y) such that

${\displaystyle \left(x-a\right)^{2}+\left(y-b\right)^{2}=r^{2}.}$

This equation, known as the Equation of the Circle, follows from the Pythagorean theorem applied to any point on the circle: as shown in the adjacent diagram, the radius is the hypotenuse of a right-angled triangle whose other sides are of length |x − a| and |y − b|. If the circle is centred at the origin (0, 0), then the equation simplifies to

${\displaystyle x^{2}+y^{2}=r^{2}.\!\ }$

Parametric form 
The equation can be written in parametric form using the trigonometric functions sine and cosine as

${\displaystyle x=a+r\,\cos t,\,}$

${\displaystyle y=b+r\,\sin t\,}$

where t is a parametric variable in the range 0 to 2π, interpreted geometrically as the angle that the ray from (a, b) to (x, y) makes with the positive x-axis.

An alternative parametrisation of the circle is:

${\displaystyle x=a+r{\frac {1-t^{2}}{1+t^{2}}}.\,}$

${\displaystyle y=b+r{\frac {2t}{1+t^{2}}}\,}$

In this parameterisation, the ratio of t to r can be interpreted geometrically as the stereographic projection of the line passing through the centre parallel to the x-axis (see Tangent half-angle substitution). However, this parameterisation works only if t is made to range not only through all reals but also to a point at infinity; otherwise, the bottom-most point of the circle would be omitted.

3-point-form 
The equation of the circle determined by three points ${\displaystyle (x_{1},y_{1}),(x_{2},y_{2}),(x_{3},y_{3})}$ not on a line is obtained by a conversion of the 3-point-form of a circle's equation

${\displaystyle {\frac {({\color {green}x}-x_{1})({\color {green}x}-x_{2})+({\color {red}y}-y_{1})({\color {red}y}-y_{2})}{({\color {red}y}-y_{1})({\color {green}x}-x_{2})-({\color {red}y}-y_{2})({\color {green}x}-x_{1})}}={\frac {(x_{3}-x_{1})(x_{3}-x_{2})+(y_{3}-y_{1})(y_{3}-y_{2})}{(y_{3}-y_{1})(x_{3}-x_{2})-(y_{3}-y_{2})(x_{3}-x_{1})}}.}$

Homogeneous form
In homogeneous coordinates, each conic section with the equation of a circle has the form

${\displaystyle x^{2}+y^{2}-2axz-2byz+cz^{2}=0.\,}$

It can be proven that a conic section is a circle exactly when it contains (when extended to the complex projective plane) the points I(1: i: 0) and J(1: −i: 0). These points are called the circular points at infinity.

Polar coordinates

In polar coordinates, the equation of a circle is:

${\displaystyle r^{2}-2rr_{0}\cos(\theta -\phi )+r_{0}^{2}=a^{2}\,}$

where a is the radius of the circle, ${\displaystyle (r,\theta )}$ is the polar coordinate of a generic point on the circle, and ${\displaystyle (r_{0},\phi )}$ is the polar coordinate of the centre of the circle (i.e., r₀ is the distance from the origin to the centre of the circle, and φ is the anticlockwise angle from the positive x-axis to the line connecting the origin to the centre of the circle). For a circle centred on the origin, i.e. r₀ = 0, this reduces to simply r = a. When r₀ = a, or when the origin lies on the circle, the equation becomes

${\displaystyle r=2a\cos(\theta -\phi ).\,}$

In the general case, the equation can be solved for r, giving

${\displaystyle r=r_{0}\cos(\theta -\phi )\pm {\sqrt {a^{2}-r_{0}^{2}\sin ^{2}(\theta -\phi )}},}$

Note that without the ± sign, the equation would in some cases describe only half a circle.

Complex plane

In the complex plane, a circle with a centre at c and radius r has the equation:

${\displaystyle |z-c|=r\,}$.

In parametric form, this can be written:

${\displaystyle z=re^{it}+c}$.

The slightly generalised equation

${\displaystyle pz{\overline {z}}+gz+{\overline {gz}}=q}$

for real p, q and complex g is sometimes called a generalised circle. This becomes the above equation for a circle with ${\displaystyle p=1,\ g=-{\overline {c}},\ q=r^{2}-|c|^{2}}$, since ${\displaystyle |z-c|^{2}=z{\overline {z}}-{\overline {c}}z-c{\overline {z}}+c{\overline {c}}}$. Not all generalised circles are actually circles: a generalised circle is either a (true) circle or a line.

Tangent lines

The tangent line through a point P on the circle is perpendicular to the diameter passing through P. If P = (x₁, y₁) and the circle has centre (a, b) and radius r, then the tangent line is perpendicular to the line from (a, b) to (x₁, y₁), so it has the form (x₁ − a)x + (y₁ – b)y = c. Evaluating at (x₁, y₁) determines the value of c and the result is that the equation of the tangent is

${\displaystyle (x_{1}-a)x+(y_{1}-b)y=(x_{1}-a)x_{1}+(y_{1}-b)y_{1}\,}$

or

${\displaystyle (x_{1}-a)(x-a)+(y_{1}-b)(y-b)=r^{2}.\!\ }$

If y₁ ≠ b then the slope of this line is

${\displaystyle {\frac {dy}{dx}}=-{\frac {x_{1}-a}{y_{1}-b}}.}$

This can also be found using implicit differentiation.

When the centre of the circle is at the origin then the equation of the tangent line becomes

${\displaystyle x_{1}x+y_{1}y=r^{2},\!\ }$

and its slope is

${\displaystyle {\frac {dy}{dx}}=-{\frac {x_{1}}{y_{1}}}.}$

Properties

• The circle is the shape with the largest area for a given length of perimeter. (See Isoperimetric inequality.)
• The circle is a highly symmetric shape: every line through the centre forms a line of reflection symmetry and it has rotational symmetry around the centre for every angle. Its symmetry group is the orthogonal group O(2,R). The group of rotations alone is the circle group T.
• All circles are similar.
  • A circle's circumference and radius are proportional.
  • The area enclosed and the square of its radius are proportional.
  • The constants of proportionality are 2πand π, respectively.
• The circle that is centred at the origin with radius 1 is called the unit circle.
  • Thought of as a great circle of the unit sphere, it becomes the Riemannian circle.
• Through any three points, not all on the same line, there lies a unique circle. In Cartesian coordinates, it is possible to give explicit formulae for the coordinates of the centre of the circle and the radius in terms of the coordinates of the three given points. See circumcircle.